Matlab’de Dört İşlem ve Temel Fonksiyonlar
Önceki yazıda Matlab’de programlamaya giriş yapılmıştı. Bu yazıda ise Matlab içerisinde dört işlem, matematiksel fonksiyonlar ve vektör tanımlama gibi konulardan bahsedeceğim. İyi çalışmalar.
Matlab’de Dört işlem ve Uygulamalar
Her programlama dilinde olduğu gibi Matlab’de de dört işlem yapmak mümkündür. Bunun için işlem yapılacak sayıları ve işlemin operatörünü yazarsak, Matlab işlemin sonucunu hesaplayıp bize çıktı olarak verecektir. Kullanılan matematiksel operatörler :
(+) = Toplam (-) = Çıkarma (/) = Bölme (*) = Çarpma
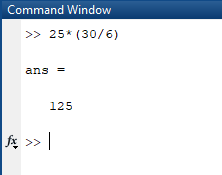
Burada dikkat edilmesi gereken bir husus da işlem önceliğidir. Matematikte bilinen dört işlem önceliği burada da aynı şekilde geçerlidir. Basitçe örnekleyecek olursak:


Matematiksel Fonksiyonlar
Matlab’de kullanılmak istenen fonksiyonun ismi yazılıp, parantez içerisine parametleri verilerek fonksiyon kullanılabilir.
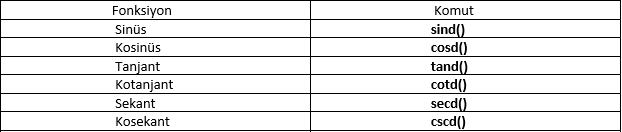
Trigonometrik Fonksiyonlar
Derece cinsinden Trigonometrik fonksiyonlar aşağıdaki tabloda verildiği gibi kullanılır.
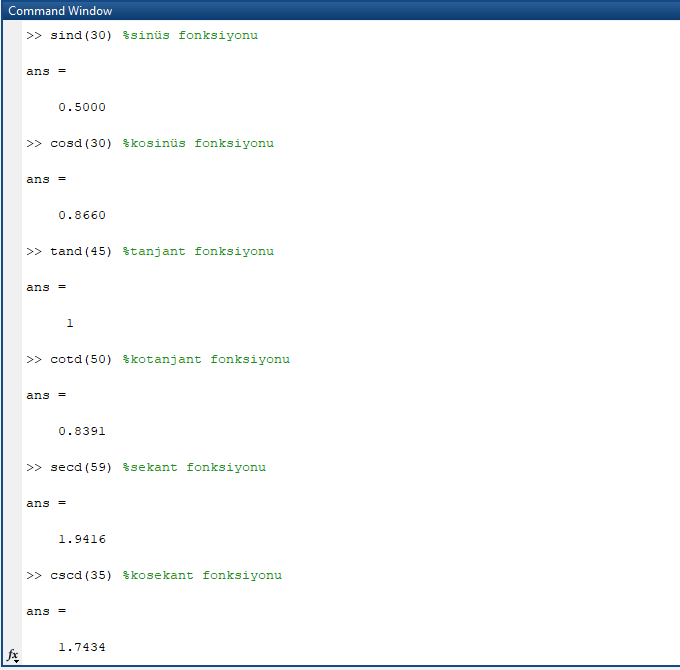
Birkaç trigonometrik fonksiyon örneği:
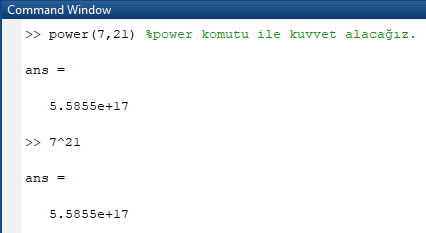
Kuvvet Alma Fonksiyonu
Matlab’de bir ifadenin kuvvetini alabilmek için power() komutu kullanılır. Komutun kullanımı power(taban, kuvvet) şeklindedir. power() komutunu kullanmadan “ ^ ” sembolünü kullanarak bir ifadenin kuvvetini hesaplanabilir. Örnek olarak:
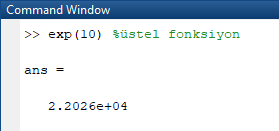
Üstel Fonksiyonlar
Tabanı euler sayısı olan fonksiyonlar mühendislikte sıklıkla kullanılır. ex fonksiyonunu hesaplamak için, Matlab’de özel bir komut olan exp( ) komutu kullanılır. Örnek olarak :
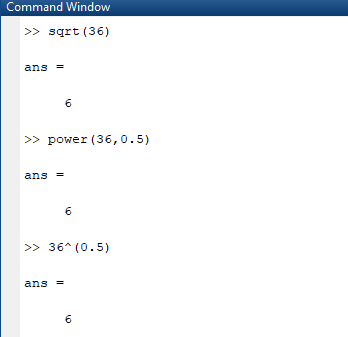
Karekök Fonksiyonu
Matlab’de karekök hesaplamak için iki yöntem kullanılır. Bunlardan ilki sqrt() fonksiyonunu kullanmaktır. Bu fonksiyon içine yazılacak ifadenin karekökünü hesaplar. İkinci yöntem ise kuvvet almaktır. Burada power() fonksiyonu ya da “ ^ ” sembolü aynı sonucu verecektir.
Örnek olarak:
Logaritmik Fonksiyonlar
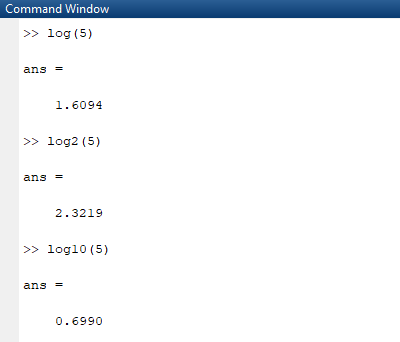
Matlab’de hesaplanmak istenen logaritmik ifade e, 2 veya 10 tabanında ise aşağıdaki tabloda yer alan komutları kullanılabilir.

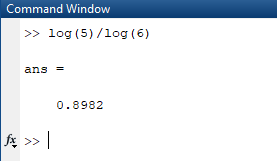
Eğer Matlab’de hesaplanmak istenen logaritmik ifadenin tabanı e, 2 ve 10 ‘dan farklıysa aşağıdaki gibi logaritma hesaplanabilir.
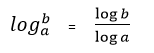
Komutları İç İçe Kullanma
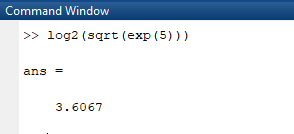
Matlab’de hesaplama yapmak için kullanılan fonksiyonlar iç içe yazılarak kullanılabilir. Bu özellik hesaplamalarda büyük bir kolaylık sağlar. Örnek olarak :
Vektör Tanımlama
Tek boyutlu sayı dizilerine, tek satırdan oluşan ya da tek sütundan oluşan matrislere vektör denir. Matlab’de vektörler kullanılarak işlem yapmak mümkündür. Bunun için ilk önce vektörlerin tanımlanması gerekir.
A = [ 1 5 9 11] şeklinde bir A vektörü tanımlanabilir. Bu bir satır vektörüdür. Çok fazla elemana sahip vektörleri böyle tanımlamak kolay olmaz. Bunun için başka bir vektör tanımlama yöntemi kullanılabilir.
a : b : c
a: Başlangıç değeri, b: Artış, c: Bitiş değeri
Bu yöntemle başlangıçtan bitişe kadar artış miktarına göre matlab kendisi bir vektör oluşturur. Örnek olarak:
0 : 1 : 10

Böylece çok fazla elemana sahip vektörler kolaylıkla tanımlanabilir.
Temel Komutlar
sort ( ) komutu: Verilen vektörün elemanlarını küçükten büyüğe doğru sıralar.

length ( ) komutu: Verilen vektörün uzunluğunu hesaplar.

linspace ( ) komutu: Girilen iki değer arasında, istenilen üçüncü bir değer kadar, eşit aralıklı bir vektör oluşturur.

sum ( ) komutu: Girilen vektörün elemanlarının toplamını verir.

prod ( ) komutu: Girilen vektörün elemanlarının çarpımını verir.

max ( ) komutu: Girilen vektörün elemanlarının arasından en büyük olanı verir.

min ( ) komutu: max() komutuna benzer olarak girilen vektörün elemanlarının arasında en küçük olanı verir.

mean ( ) komutu: Girilen vektörün elemanlarının ortalamasını verir.