Matlab’de Polinom Türevi ve Denklem Çözme
Bu yazıda sizlere Matematik’te sıklıkla karşımıza çıkan polinomların, türevlerinin ve denklem çözme problemlerinin Matlab’de nasıl hesaplandığından bahsedeceğim.
Polinom Türevi
Sabit katsayılı n. dereceden bir polinomun genel hali:
an xn + an-1 xn-1 + an-2 xn-2 + … + a1 x + a0 gibidir.
Bu polinomun türevi,
an n xn-1 + an-1 (n-1) xn-2 + an-2 (n-2) xn-3 + … + a1 şeklindedir.
Buna göre bir polinomun türevi alınabilir. Ancak bu türevi Matlab ile hesaplamak mümkündür. Bir polinomun Matlab’de türevini hesaplamak için polyder() fonksiyonu kullanılmalıdır. Bu fonksiyon içerisine polinomun katsayılarından oluşan satır vektörü yazıldığında sonuç olarak polinomun türevinin katsayılarından oluşan satır vektörü elde edilir. Örnek olarak P(x) = 5 x4 + 10 x3 + 3 x2 + x + 5 polinomunun türevini Matlab’de hesaplayalım.
INPUT:
>>p = [5 10 3 1 5]
OUTPUT:
p =
5 10 3 1 5
INPUT:
>>polyder(p)
OUTPUT:
ans = 2 >> % türev 20 x3 + 30 x2 + 6 x + 1 olarak elde edilir.P(x) = 4 x2 + 5x + 3 ve P(x) = 5 x2 + 6 x + 5 iki polinomun çarpımının türevini Matlab’de hesaplayalım:
INPUT:
>>p1 = [4 5 0 3]
OUTPUT:
p1 =
4 5 0 3
INPUT:
>>p2 = [5 6 4]
OUTPUT
p2 =
5 6 4
INPUT:
>>carpim = conv(p1,p2)
OUTPUT:
carpim = 20 49 46 35 18 12
INPUT:
>>polyder(carpim)
OUTPUT:
ans = 100 196 138 70 18
>> %Polinomun türevi: 100 x4 + 196 x3 + 138 x2 + 70 x + 18Parçalı Kesre Ayırma
Şimdi residue( ) fonksiyonundan bahsedelim. Bu fonksiyon tam kesir halinde verilen bir polinomu parçalı (basit) kesir şeklinde yazmamızı sağlıyor. A(x) ve B(x) iki polinom ise,
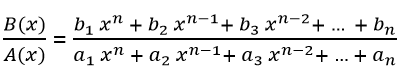
şeklindeki kesir ifadesini residue( ) fonksiyonu ile parçalı kesir halinde yazacağız. Öncelikle pay ve paydadaki polinomların katsayılarından oluşan satır vektörünü Matlab’de tanımlayalım.
b = [b1 b2 b3 b4 … bn]
b = [a1 a2 a3 a4 … an] şeklinde tanımlanır.
residue(b, a) fonksiyonunun kullanımı [r, p, k] = residue(b,a) gibidir. Burada r, n’inci parçalı kesrin payı, p, n’inci parçalı kesrin paydası ve k’da sabit terimdir. Böylece verilen tam kesrin parçalı hali aşağıdaki gibi olur:
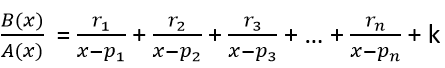
Örnek olarak A(x)/B(x) = (x2 -2x+1)/ (x2 – 1) kesrini parçalı kesre ayıralım. Bu işlemi aşağıda görüldüğü gibi yapabiliriz:
INPUT:
>> b = [1 -2 1]
OUTPUT:
b =
1 -2 1
INPUT:
>>a = [1 0 -1]
OUTPUT:
a = 1 0 -1
INPUT:
>>[pay,payda,sabit] = residue(b,a)
OUTPUT:
pay = -2 0
payda = -1 1
sabit = 1
>> %Düzenlersek (-2/(x+1)) + (0/(x-1)) + 1 = (x-1)/(x+1) olarak bulunur.
Polinom ile ilgili daha fazla örnek çözümünü sonraki yazılarımızda paylaşmayı düşünüyorum. Şimdi ise Matlab’de birinci dereceden denklemlerin nasıl çözülebildiğine bakalım. Ancak denklem çözümüne geçmeden önce sizlere birkaç komuttan ve sembolik ifadeden bahsetmek istiyorum. Matlab’de integral, türev, limit ve denklem çözümü işlemleri hesaplarken sembolik nesnelere ihtiyacımız olur. Çünkü bu işlemlerde kullanacağımız fonksiyonlar sembolik nesneler ile çalışır. sym ve syms komutları bir değişkeni sembolik nesne yapmaya yarar. Örnek olarak: >> syms x; yazarsak, x değişkeni artık sembolik nesnedir.
pretty() ve simplify() Komutları
Aynı zamanda yaptığımız işlemlerin sonuçlarının daha anlaşılır ve sade olarak görülmesi için pretty() ve simplify( ) komutlarını kullanabiliriz. pretty( ) komutu, sembolik nesneden oluşan sonucun ekranda daha net olarak görünmesini sağlarken, simplify( ) komutu ise sonucu sadeleştirmek için kullanılır. Bu komutların kullanışlarını denklem çözümünde göstereceğim. Burada son olarak expand( ) ve factor( ) komutlarından bahsedeyim. expand( ) komutu, sembolik nesneden oluşan polinomların kuvvet açılımlarını yapmak içini factor( ) komutu ise kuvvet açılımı yapılmış polinomları eski haline dönüştürmek için kullanılır. Örnek olarak (x+1)9 ifadesinin kuvvet açılımını yapalım.
INPUT:
>>syms x;
>>kuvvet = (x+1)^9
OUTPUT:
kuvvet =
(x + 1)^9
INPUT:
>>expand(kuvvet)
OUTPUT:
ans =
x^9 + 9x^8 + 36x^7 + 84x^6 + 126x^5 + 126x^4 + 84x^3 + 36x^2 + 9x + 1
INPUT:
>>syms x;
>>acilim = x^9 + 9x^8 + 36x^7 + 84x^6 + 126x^5 + 126x^4 + 84x^3 + 36x^2 + 9x + 1
OUTPUT:
acilim =
x^9 + 9x^8 + 36x^7 + 84x^6 + 126x^5 + 126x^4 + 84x^3 + 36x^2 + 9x + 1
INPUT:
>>factor(acilim)
OUTPUT:
ans =
[ x + 1, x + 1, x + 1, x + 1, x + 1, x + 1, x + 1, x + 1, x + 1]DENKLEM ÇÖZÜMÜ
solve() komutu: Verilen denklem ya da denklemlerin, sembolik nesnelerden yararlanarak köklerini bulan komuttur. Komut solve(BURAYA DENKLEM YAZILIR) şeklinde kullanılır. Öncelikle tek bilinmeyenli denklem örneklerine bakalım. Örnek olarak x2 – 6 x – 3 = sqrt(3 x – 5) denkleminin çözümünü solve komutunu kullanarak bulalım. Bu hesaplama işlemi için aşağıdaki işlemler yapılabilir:
INPUT:
>>syms x;
>>cozum = solve(x^2-6x-3-(3x-5)^(1/2));
>>cozum
OUTPUT:
cozum =
7
>>
Bir başka örnek için e(x2 + 3 x) – 15 x = 0 denklemini Matlab’de çözelim. Bu ifadeyi Matlab’de aşağıda görüldüğü gibi çözebiliriz:
INPUT:
>>syms x;
>>cozum = solve(exp(x^2+3*x)-15);
>>cozum
OUTPUT:
cozum =
(4log(15) + 9)^(1/2)/2 - 3/2,(4log(15) + 9)^(1/2)/2 - 3/2
>> İki ya da daha fazla bilinmeyenli denklemlerin çözümlerinde de aynı şekilde solve( ) komutu kullanılabilir. Bunun yanı sıra iki ya da daha fazla bilinmeyenli lineer denklemlerde solve( ) komutu kullanılmadan da çözüm bulmak mümkündür. Örnek olarak:
2x + 4y = 10
3x + 5y = 13
lineer denklem sisteminin çözümünü bulalım.
Bunun için ilk olarak verilen denklemleri matris biçiminde yazalım. Bunu aşağıdaki gibi yazabiliriz:
[2 4 ; 3 5 ].[x ; y] = [10 ; 13]
Bu ifadede çarpma işlemi yapılırsa yukarıdaki denklem sistemi elde edilir. Eşitliğin iki tarafını soldan [2 4 ; 3 5]-1 ile çarpalım. Böylece,
[x ; y] = [2 4 ; 3 5]-1 . [10 ; 13] eşitliği elde edilir.
Eşitliğin sağ tarafındaki işlem yapıldığında bulmak istediğimiz x ve y değerlerine ulaşırız. Öncelikle Matlab’de eşitliğin sağ tarafında bulunan matrisleri tanımlayalım. Ardından [2 4; 3 5] matrisinin tersiyle [10 ; 13] sütun vektörünü çarparak x ve y’yi elde edelim. Bu işlemin Matlab çıktısı aşağıdaki gibidir:
INPUT:
>>A = [2 4;3 5];
>>A_tersi = inv(A)
OUTPUT:
A_tersi =
-2.5000 2.0000
1.5000 -1.0000
INPUT:
>>B = [10;13];
>>cozum = A_tersi*B
OUTPUT:
cozum =
1.0000 2.0000 >>Ancak bu denklem solve( ) komutu ile daha kolay bir şekilde çözülebilir. Aşağıda görüldüğü gibi çözüme ulaşılabiliriz:
INPUT:
>>syms x y;
>>[xc,yc] = solve(2x+4y-10,3x+5y-13)
OUTPUT:
xc =
1
yc =
2
>>Başka bir yazıda Matlab’den bahsetmeye devam edeceğim.