Matlab’de Matematiksel İşlemler
Bu yazıda sizlere limit, türev, integral ve diferansiyel denklemlerin Matlab’de nasıl çözüldüğünden bahsedeceğim.
Matlab’de Limit
Matematikte çok önemli bir yere sahip olan limit problemlerini Matlab’de çözmek mümkündür. Bunun için limit() komutunu kullanmamız gerekir. Komutun içerisine yazmamız gereken fonksiyon sembolik nesnelerden oluşmalıdır. Eğer sembolik nesne ile ilgili herhangi bir fikriniz yoksa buradan bir önceki yazımızı okumanızı tavsiye ederim. Komutun kullanılışı,
limit(fonksiyon,değişken,değer,left-right)
şeklindedir. Burada eğer fonksiyonumuz x değişkenine bağlı ise değişken yerine x yazılır. x değişkeninin yaklaşmaya çalıştığı değer b ise değer yerine b yazılmalıdır. Eğer ki b değerine b+(sağdan) ya da b–(soldan) yaklaşıyorsak left veya right değerlerinden biri yazılmalıdır.
![]()
Limit x→∞ ise değer yerine inf, x→-∞ ise –inf yazılmalıdır. Böylece limit bulunmuş olacaktır. Birkaç örnek yapalım.
Örnekler
![]()
INPUT:
>> syms x;
>> f = (7^(2*x+1) - 49*(7^(x+3)))/(49^(x-1) + 77);
>> sonuc = limit(f,x,inf);
>> sonuc
OUTPUT:
sonuc =
343 ![]()
INPUT:
>> syms x;
f1 = (9*x)/abs(x);
>> sonuc1 = limit(f1,x,0,'left');
>> sonuc1
OUTPUT:
sonuc1 =
-9 INPUT:
>> syms x;
>> f2 = (3*(x^2) - 3)/ (x-1);
>> sonuc2 = limit(f2,x,1);
>> sonuc2
OUTPUT:
sonuc2 =
6 ![]()
INPUT:
syms x a;
f3 = ((x^3) - (a^3))/(sin(3x -3a));
sonuc3 = limit(f3,x,a) ;
sonuc3
OUTPUT:
sonuc3 =
a^2 INPUT:
>> syms x;
>> f4 = (6*(x^2) + 5*x + 3) / (9*x);
>> sonuc4 = limit(f4,x,1,'right');
>> sonuc4
OUTPUT:
sonuc4 =
14/9 Matlab’de Türev
Mühendislik ve matematik başta olmak üzere birçok alanda karşımıza çıkan türev problemlerini matlab ile çözmek için diff() komutunu kullanmamız yeterlidir. Türevini hesaplama ihtiyacı duyduğumuz fonksiyonu diff() komutuna yazarken, fonksiyonun değişkenini matlab’de sembolik nesne olarak tanımlamış olmamız gerekir. Komutun kullanışı diff(fonksiyon,derece,değişken) şeklindedir. Fonksiyon ve değişken kısımlarına neler yazılması gerektiği limit() komutundan biliyoruz. Derece yerine ise fonksiyonun kaçıncı mertebeden türevinin olmaması gerektiği yazılmalıdır. Örnek olarak f(x) fonksiyonunun 2.mertebeden türevi hesaplanmak isteniyorsa komut satırına diff(f(x),2,x) yazılması yeterlidir. Matlab sonucu bize çıktı olarak gösterecektir.
Örnekler
![]()
INPUT:
>> syms x;
>> f = 7*(x^6) + 6*(x^5) + 10*(x^4) + 2*(x^2) + 1;
>> sonuc = diff(f,1,x);
>> sonuc
OUTPUT:
sonuc =
42*x^5 + 30*x^4 + 40*x^3 + 4*x ![]()
INPUT:
>>syms x;
>>f = (x^2)tan(x) + (cos(4(x^2)))^2;
>>sonuc = diff(f,1,x);
>>sonuc
OUTPUT:
>>sonuc =
>>2xtan(x) + x^2(tan(x)^2 + 1) - 16xcos(4x^2)sin(4x^2) ![]()
INPUT:
>>syms x;
>>f = exp(x)(sin(5x));
>>sonuc = diff(f,3,x);
>>sonuc
OUTPUT:
>>sonuc =
>>-110cos(5x)exp(x) - 74sin(5x)exp(x) ![]()
INPUT:
>>syms x;
>>f = (1)/(2 + sin(2x));
>>turevin_sonucu = diff(f,2,x);
>>sonuc = subs(turevin_sonucu,5); %x = 5 noktasındaki 2.türevin sonucuna bakıyoruz.
>>sonuc
>>OUTPUT:
>>sonuc = (4sin(10))/(sin(10) + 2)^2 + (8*cos(10)^2)/(sin(10) + 2)^3 Matlab’de İntegral
Matlab’de int() komutunu kullanarak herhangi bir integral probleminin çözümünü bulabiliriz. Bu komutun içerisine yazacağımız fonksiyonun değişkeninin yine önceki iki komut gibi sembolik nesne olarak tanımlanmış olması gerekir. int() komutu ile belirli veya belirsiz integraller çözdürülebilir. Eğer belirsiz integral çözmek istiyorsak int(fonksiyon) komutunu kullanmalıyız. Fakat belirli integral çözmek istiyorsak int(fonksiyon,başlangıç değeri,bitiş değeri) komutunu kullanmamız yeterlidir. Bazı durumlarda matlab integrali hesaplayamayabilir. Bu durumda quad() komutunu kullanarak integralin yaklaşık değerini hesaplayabiliriz.
Örnekler
![]()
INPUT:
>> syms x;
>> f = 3*(x^5) + 2*(x^2) + 1;
>> sonuc = int(f);
OUTPUT:
sonuc =
x^6/2 + (2*x^3)/3 + x ![]()
INPUT:
>> syms x;
>> f = (x^2)*sin(x);
>> sonuc = int(f);
>> sonuc
OUTPUT:
sonuc =
2*x*sin(x) - cos(x)*(x^2 - 2) ![]()
INPUT:
>>syms x;
>>f = (2)/(2 + 3*x);
>>sonuc = int(f,0,1);
>>sonuc
OUTPUT:
>>sonuc =
>>log(50^(1/3)/2) ![]()
INPUT:
>>syms x;
>>f = ((sin(3x))^2)cos(x);
>>sonuc = int(f,0,pi/2);
>>sonuc
OUTPUT:
>>sonuc =
>>17/35 Bu tip integral hesaplamalarının dışında iki katlı ya da üç katlı integraller hesaplanabilir.
Çok Katlı İntegraller
![]()
![]()
Örnekler
![]()
INPUT:
>>syms x y;
>>f = (x^2) + (y^2);
>>sonuc = int(int(f,y,0,x/4),x,0,3);
>>sonuc
OUTPUT:
>>sonuc =
>>1323/256 ![]()
INPUT:
>>syms x y z;
>>f = (x^2)(y^2)(z^2);
>>sonuc = int(int(int(f,x,0,3),y,0,5),z,0,4);
>>sonuc
OUTPUT:
>>sonuc =
>>8000Bu şekilde matlab’de herhangi bir integral problemini hesaplayabiliriz. Son olarak diferansiyel denklem çözümlerinden bahsedip yazıyı sonlandıracağım.
Matlab’de Diferansiyel Denklemler
Limit, türev, integral gibi matematik, fizik ve mühendislik alanlarında önemli bir yere sahip olan diferansiyel denklemleri matlab üzerinde çözebilmek mümkündür. Bilinmeyen fonksiyonun bir bağımsız değişkene bağlı olduğu adi diferansiyel denklemleri çözmek için Dsolve() komutu kullanılabilir. Komut içerisindeki d/dt ifadesi ‘D’ ile temsil edilir. Dsolve komutunun kullanımı Dsolve(‘Diferansiyel denklem’,başlangıç koşulları) şeklindedir. Diferansiyel denklemin matlab’de temsili aşağıdaki gibidir:
![]()
Örnekler
![]()
INPUT:
>>syms x y;
>>x=dsolve('D2y-6Dy+25y=0');
>>x
OUTPUT:
>>x =
>>C1cos(4t)exp(3t) + C2sin(4t)exp(3t) ![]()
INPUT:
>>syms x y t;
>>x=dsolve('D2y-Dy-2y=exp(4t)');
>>x
OUTPUT:
>>x =
>>exp(4t)/10 + C1exp(2t) + C2exp(-t) ![]()
![]()
INPUT:
>>syms x y t;
>>x=dsolve('D2y+8Dy+2y+1=t','y(0)=0','Dy(0)=-1');
>>x
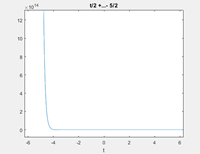
>>ezplot(x)
OUTPUT:
>>x =
>>t/2 + exp(t(14^(1/2) - 4))((1714^(1/2))/56 + 5/4) + (14^(1/2)exp(-t(14^(1/2) + 4))(5*14^(1/2) - 17))/56 - 5/2