Kısaca hatırlamak gerekirse; kompleks mekanik sistemleri veya yapıları analiz etmek söz konusu olduğunda, mühendisler ve bilim insanları genellikle bu sistemleri basitleştirilmiş bir şekilde temsil eden matematiksel modellere dayanırlar.
Modelleme dünyasında, düğümler, elemanlar ve serbestlik dereceleri doğru ve verimli modeller oluşturmada önemli bir rol oynayan temel kavramlardır.
İçerikler
Düğümler
Düğümler, temel olarak bir model oluşturmak için bir araya getirilen elemanların bağlandığı noktalardır. Başka bir deyişle, sistem veya yapıların farklı bileşenlerinin birbirine bağlandığı fiziksel konumları temsil ederler.
Elemanlar
Elemanlar, farklı geometrik şekillere sahip olabilirler ve farklı tiplerde sınıflandırılabilirler. Bunlar arasında çubuk elemanlar, düzlem elemanlar ve kabuk elemanlar bulunur.
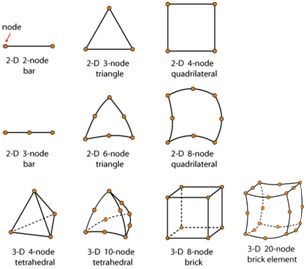
Çubuk elemanlar (rods, bars, poles, beams), silindirik veya dikdörtgen prizma gibi basit geometrik şekillere sahiptir ve iki düğüm arasındaki bağlantıyı temsil eder. Genellikle yapılarda çerçeve veya kirişlerin modellenmesinde kullanılırlar. Makine elemanı olarak ise kafes (truss) yapılarda karşımıza çıkar.
Düzlem elemanlar (plates), ince bir düzlem şekline sahiptir ve düzlem gerilmeleri modeller. Bu elemanlar, genellikle levhalar, duvarlar, plakalar veya tabakalar gibi yapı bileşenlerinin modellenmesinde kullanılırlar. Düzlem elemanlarının örnekleri arasında üçgen veya dikdörtgen şeklinde elemanlar yer alabilir. Kabuk elemanlar (shells), üç boyutlu yüzeylere sahip elemanlardır. Kabuk elemanları, çatılar, kubbe veya silolar gibi çeşitli yapı bileşenlerinin modellenmesinde kullanılır. Kabuk elemanlarının örnekleri arasında küresel, silindirik veya konik şekilli elemanlar yer alabilir.
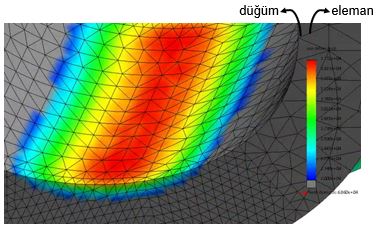
Bu eleman tipleri, modellemede kullanılan farklı geometrik şekillere sahip elemanları ifade etmektedir. Farklı eleman tiplerinin seçimi, yapı bileşenlerinin gerçekçi bir şekilde modellenmesine ve doğru sonuçlar elde edilmesine yardımcı olur.
Serbestlik Derecesi
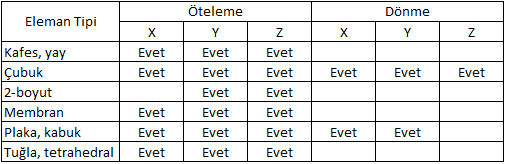
Serbestlik derecesi (degrees of freedom), bir elemanın hareket edebileceği veya dönebileceği yolları ifade eder. Bunlar dönme (rotation) ve öteleme (translation) hareketi olarak ifade edilebilir. Bir elemanın her bir serbestlik derecesi, bir düğümün konumundaki değişime bağlıdır. Bir elemanın serbestlik derecesi, elemanın bir düğüme bağlanabilecek en fazla sayıda hareket derecesini belirler.
Her elemanın farklı sayıda serbestlik derecesi olabilir. Örneğin, bir çubuk elemanının iki serbestlik derecesi vardır: öteleme ve dönme. Bir düzlem elemanının üç serbestlik derecesi vardır: iki düzlemdeki gerilme ve düzlemler arasındaki kayma. Kabuk elemanlarının ise altı serbestlik derecesi vardır: x, y ve z eksenlerindeki hareket ve x, y ve z eksenlerindeki dönme hareketleri.
Serbestlik dereceleri, yapının davranışının anlaşılması ve modellenmesi için önemlidir. Bu kavramın doğru anlaşılması, yapıların analizinde ve tasarımında önemli bir rol oynar. Farklı disiplinlerde serbestlik dereceleri farklı formlar halinde olabilir. Örneğin katı mekaniğinde bir elemanın serbestlik derecesi yer değiştirme (displacement), dönme (rotation) olarak ifade edilebilirken; ısı transferi veya termal analiz söz konusu olduğunda serbestlik derecesi sıcaklık (temperature) olur.
Sınır Koşulları
Sınır koşulları, bir yapı elemanının veya bir makine elemanının hareketinin sınırlandığı yerlerde belirlenen koşullardır. Mekanikte sınır koşulları, bir elemanın yerleştirildiği ve diğer elemanlarla olan etkileşimini tanımlayan önemli bir konudur. Sınır koşulları, elemanların hareketine, deformasyonuna ve gerilimine etki eder ve doğru bir şekilde tanımlanmadığı takdirde yapı elemanlarının davranışı yanlış yorumlanabilir.
Sınır koşulları, üç temel tiptedir: sabitlenmiş sınır koşulları, hareketli sınır koşulları ve yük sınır koşulları.
Sabitlenmiş sınır koşulları
Sabitlenmiş sınır koşulları, bir elemanın hareketinin tamamen sınırlandığı koşullardır. Bu koşul, elemanın yer değiştirmesi veya döndürülmesi gibi herhangi bir hareketini engeller. Bu tip sınır koşulları genellikle yapının temelinde veya sabitlenmiş bir duvarda bulunur.
Hareketli sınır koşulları
Hareketli sınır koşulları, bir elemanın hareketinin kısmen sınırlandığı koşullardır. Bu koşullar, elemanın yer değiştirme veya döndürülmesini belli bir dereceye kadar engeller, ancak elemanın kalan hareketi serbesttir. Bu tip sınır koşulları, bir elemanın bir diğer elemana veya bir yapıya sabitlenmesinde kullanılır.
Yük sınır koşulları
Yük sınır koşulları, bir elemanın üzerine uygulanan yükün etkisini belirler. Bu koşullar, elemanın deformasyonuna ve stresine etki eder. Elemanın deformasyonu, elemanın üzerindeki yükün büyüklüğüne bağlıdır ve yük arttıkça elemanın deformasyonu da artar.
Sınır koşulları, yapı elemanlarının doğru bir şekilde modellenmesi ve analiz edilmesi için kritik öneme sahiptir. Yanlış sınır koşulları, elemanların davranışını yanlış yorumlamaya ve yapı sisteminin yanlış bir şekilde modellenmesine neden olabilir. Bu nedenle, sınır koşulları, yapı elemanlarının doğru bir şekilde analiz edilmesi için doğru bir şekilde belirlenmelidir.
Bu sınır koşulları temel olarak üç şekilde ifade edilebilir: sınır koşulunun tanımlandığı Dirichlet tipi koşullar, bu sınır koşuluna bağlı bir gradyan olarak ifade edilen Neumann tipi koşullar ve bu ikisinin kombinasyonu olan, bağımlı bir değişkenin ve bu değişkenin gradyanını içeren Robin tipi koşullar.
Katı mekaniğinden örnek verecek olursak Dirichlet tipi koşul – yer değiştirme (displacement), Neumann tipi koşul – çekiş ya da gerilme (traction, stress), Robin tipi koşul ise yay (spring) olur.
Sonlu elemanlar analizinde en temel tanımlamalardan biri olan bu terimlerin öğrenilmesi, analizin doğru kavranması için önemlidir.
Sonraki yazılarda sonlu elemanlar analizi üzerine yoğunlaşarak; katı mekaniği, malzeme mekaniği gibi konular üzerinde daha teknik ve detaylı yazılarla devam edeceğiz.

