Bu yazıda sitemize de adını veren, Matematiğin en önemli sabitlerinden birisi kabul edilen Pi sayısından bahsedeceğim.
İçerikler
Pi sayısı nedir?
Pi sayısı herhangi bir dairenin çevresinin, çapına olan oranıdır. Çemberin boyutu fark etmeksizin bu oran her zaman pi’ye eşittir. 1647’ye kadar evrensel bir adı veya sembolü yoktu Matematikçiler 1700’lü yıllarda Yunanca “çevre” anlamına gelen περιμέτρου (perimetros) kelimesinin ilk harfi olan π’yi sembol olarak kullanmaya başlamışlardır. William Jones tarafından 1706 yılında tanıtılan sembol, 1737’de İsviçreli matematikçi Leonhard Euler’in sembolü benimsemesinin ardından kullanımı popülerleşti.

William Jones (1675-1749)

Leonhard Euler (1707-1783)
Pi sayısı nasıl hesaplanır?
1767’de İsviçreli matematikçi Johann Heinrich Lambert pi’nin irrasyonel olduğunu kanıtladı ve 1882’de ise Ferdinand von Lindemann pi’nin sonsuz olduğunu kanıtladı. Bu bulgu önemlidir, çünkü bu noktaya kadar “çemberin karesini almak” olarak bilinen eşit alanlı bir kare ve bir daire oluşturulabileceğine inanılıyordu. Pi’nin sonsuz olduğunu kanıtlamak bunun mümkün olmadığını gösterdi. Pi irrasyonel olduğundan diğer tüm irrasyonel sayılar gibi bir kesir (basit veya kaba kesir olarak da bilinir) olarak gösterilemez. π sonsuz olduğu için cebirsel değildir. Bu da bize π’nin ikinci derecen bir irrasyonel olamayacağını gösterir. İkinci dereceden bir irrasyonel olamaması π’nin periyodik bir sürekli kesire de sahip olmadığını ifade eder. Ancak, pi dahil her irrasyonel sayı, sürekli kesir adı verilen sonsuz bir iç içe geçmiş kesirler dizisi ile temsil edilebilir:
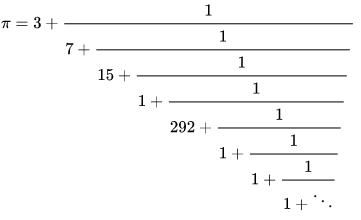
Kesrin herhangi bir noktada kesilmesi, π için rasyonel bir yaklaşıklık verir; bunların ilk dördü 3, 22/7, 333/106 ve 355/113’tür. Bu şekilde üretilen her yaklaşım, en iyi rasyonel yaklaşımdır; yani, her biri aynı veya daha küçük paydaya sahip diğer herhangi bir kesirden π’ye daha yakındır.
Pi Sayısının Tarihi
Erken Dönem Tarihi
Pi’nin tarihi, MÖ 2000 yılına kadar uzanır. Bu dönemlerde Babilliler ve Mısırlılar π’yi kullanmışlardır. Babilliler (yaklaşık MÖ 2000) pi’yi yaklaşık olarak 3,125 kullandılar; bu değer, bir daire içine yazılmış bir altıgenin çevresini hesaplayarak, dairenin çevresine oranının 24/25 olduğunu varsayarak elde ettikleri bir değerdi. Rhind Papirüsü (yaklaşık MÖ 1650) bize eski Mısırlıların 256/81 veya yaklaşık 3.16045 değerini kullandıklarını gösteriyor. Hem Babilliler hem de Mısırlılar pi değerine ilişkin kaba sayısal tahminlere sahipti ve daha sonra Antik Yunanistan’daki matematikçiler, özellikle Arşimet, pi’yi hesaplamak için algoritmik bir yaklaşım kullanan ilk kişi oldu. Arşimet, bir çemberin içine bir çokgen ve çemberin dışına ikinci bir çokgen çizdi. Sonra sürekli olarak çokgen ekleyerek çemberin şekline gittikçe yaklaştı. Böylece 96 kenarlı çokgenlere ulaşarak 223/71 <π <22/7 veya yaklaşık 3.1418 gibi ortalama bir değer elde etti. Arşimet ayrıca bir dairenin alanının, yarıçapının karesine oranının aynı sabit olduğunu ve bir dairenin alanının, tabanı bu dairenin çevresine ve yüksekliği ise yarıçapına eşit bir üçgenin alanına eşit olduğunu kanıtlamıştır. Benzer bir yaklaşım, Çinli matematikçi ve gök bilimci olan Zu Chongzhi (429-501) tarafından da kullanıldı. Bir çemberin çevresinin çapına oranının değerini 355/113 olarak hesapladı.
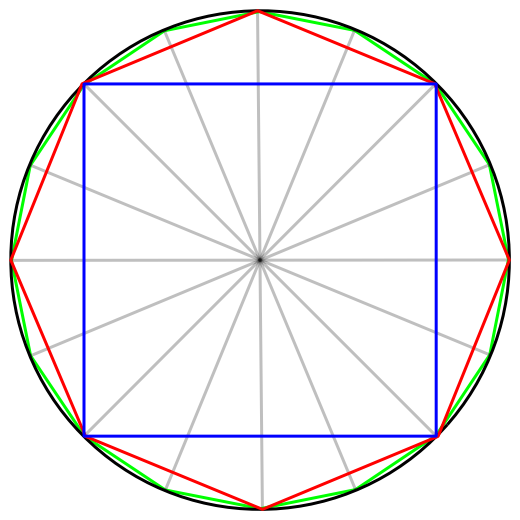

Görsel Kaynak: piday
MS 5.yüzyılda geometrik teknikleri kullanarak Hintli matematikçiler π sayısında beş haneye yaklaşırken, Çinli matematikçiler yedi basamaklı bir yaklaşım yaptı. MS 265 civarında, Wei Hanedanı matematikçisi Liu Hui, poligon tabanlı yinelemeli bir algoritma yarattı ve bunu 3.072 kenarlı bir çokgenle kullanarak 3.1416 değerini elde etti. Liu daha sonra hesaplamanın daha hızlı bir yöntemini icat etti ve ardışık çokgenlerin alanlarındaki farklılıkların 4 faktörlü bir geometrik seri oluşturmasından yararlanarak 96 kenarlı bir çokgenle 3.14 değerini elde etti. Hintli gök bilimci Aryabhata, Āryabhaṭīya’sında (MS 499) 3,1416 değerini kullandı. Fibonacci 1220’de, Arşimet’ten bağımsız bir poligonal yöntem kullanarak 3.1418’i hesapladı.
15. yüzyıl
Fars gök bilimci Jamshad al-Kāshī, 1424 yılında pi’nin yaklaşık 16 ondalık basamağına eşdeğer olan 9 altmışlık basamak üretti. Bu basamak değeri yaklaşık 180 yıldır dünya rekoru olmuştur. Madhava, 1400 civarında π’nin 11 hanesini tahmin etmek için sonsuz seriler kullandı, ancak bu değer, çokgen bir algoritma kullanarak Pers matematikçi Jamsh Jamd al-Kāshī tarafından yaklaşık 1430’da iyileştirildi.
16. ve 17. yüzyıl
Fransız matematikçi François Viète 1579’da 9 basamak elde etti. Flaman matematikçi Adriaan van Roomen ise 1593’te 15 ondalık basamağa ulaştı. 1596’da Hollandalı matematikçi Ludolph van Ceulen 20 haneye ulaştı, bu rekor daha sonra 35 haneye yükseldi. 1630’da Avusturyalı gökbilimci Christoph Grienberger, 1040 kenarlı çokgenleri kullanarak 38 basamaklı pi hesapladı.
On sekizinci yüzyıla gelindiğinde Fransız matematikçi Georges Buffon π’yi olasılığa dayalı hesaplamanın yolunu buldu (Buffon’un iğne problemi veya Buffon’s needle problem). Isaac Newton, 16 ondalık basamağı hızlı bir şekilde hesaplamak için binom teoremini kullanmış, 20. yüzyılın başlarında, Hintli matematikçi Srinivasa Ramanujan, daha sonra bilgisayar algoritmalarına dahil edilen pi hesaplamanın olağanüstü verimli yollarını geliştirmiştir.
π’nin hesaplanmasında, 16. ve 17. yüzyıllarda sonsuz seri tekniklerinin geliştirilmesi ile devrim yaratıldı. Sonsuz seriler, matematikçilerin π’nin hesaplamasını Arşimet ve geometrik teknikler kullanan diğerlerinden çok daha yüksek hassasiyetle yapmalarına olanak sağladı. π’yi hesaplamak için kullanılabilecek sonsuz bir dizinin ilk yazılı açıklaması Hintli gök bilimci Nilakantha Somayaji tarafından MS 1500 civarında Tantrasamgraha’da Sanskritçe dizesinde ortaya konmuştur. Bu açıklama seri kanıt olmadan sunulmasına rağmen kanıtlar ancak MS 1530 civarında daha sonraki bir Hint eserinde sunuldu. Nilakantha ise, bu seriyi daha önceki Hintli matematikçi Madhava’ya atfeder. Günümüzde Madhava serisi veya Gregory-Leibniz serisi olarak anılan sinüs, tanjant ve kosinüs serileri de dahil olmak üzere birkaç sonsuz dizi tanımlanmıştır.

Görsel Kaynak : piday
Yakın tarih ve günümüz
20. yüzyılın başlarına gelindiğinde π’nin yaklaşık 500 basamağı biliniyordu. Modern teknolojik gelişmelerle, π’nin 31 trilyon basamağı hesaplandı. Bununla birlikte, gözlemlenebilir evrenimizdeki tüm hesaplamaları neredeyse hiç hata olmadan yapabilmek için yalnızca π’nin ilk 39 basamağına ihtiyacımız vardır.
İlki 1988 yılında Larry Shaw tarafından organize edilen Pi Günü, her yıl 14 Mart’ta kutlanmaktadır.
Hepimizin Pi Günü kutlu olsun! 🙂
Pi’nin Kullanım Alanları
Pi, yayların uzunluklarını veya diğer eğrileri, elips alanlarını ve diğer eğimli yüzeyleri ve birçok katı hacmini içeren çeşitli matematik problemlerinde ortaya çıkar. Ayrıca, açısal hız, sarkaçların hareketi, sicimlerin titreşimi ve alternatif elektrik akımları gibi periyodik olayları tanımlamak için çeşitli fizik ve mühendislik formüllerinde kullanılır.


Bu yazıyı yazanın bilgilerine ulaşamıyoruz
Merhabalar Pi Sayısı Nedir? Tarihi ve Önemi yazısının yazarının adını ve yazma tarihini öğrenebilir miyim? Makalemde atıf yapmak istiyorum da
Merhaba Fatih bey, konu ile ilgili e-posta adresiniz üzerinden iletişime geçtik.